| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- 웹해킹기초
- GIT
- 뷰
- 웹해킹
- 워게임
- 웹개발
- 자료구조
- node
- 워게임추천
- mongoose
- 웹기초
- node.js
- NavBar
- gitbash
- MongoDB
- Express
- materialize
- 써니나타스
- 자바기초
- CTF
- 그래프
- 자바
- bootstrap
- 포렌식워게임
- 포렌식
- 이진탐색트리
- wargame.kr
- 이진트리
- 자바문제풀이
- nodeJS
- Today
- Total
보안 전공생의 공부
트리 (1) | 트리, 이진트리 본문
출처 : book.naver.com/bookdb/book_detail.nhn?bid=10896666
C로 배우는 쉬운 자료구조
단계별 그림과 삽화로 이론을 다지고 C 언어로 구현해 보는 자료구조 입문서 자료를 구조화하는 다양한 방법을 단계별 그림과 삽화를 곁들여 쉽게 설명하고, 자료구조의 핵심 알고리즘을 C 프로
book.naver.com
목차
01 트리에 대해
02 이진트리에 대해
03 이진트리의 구현과 순회
04 이진탐색트리, AVL 트리
05 히프
01. 트리에 대해
◆ 트리 (tree) : 1 : n 비선형 자료구조 & 계층형 자료구조(hierarchical data structure)
ex) 가족관계를 나타내는 가계도 !
(짱구네 신씨집안 가계도를 제 맘대로 만들어보았습니다)

· -로 연결된 가족 구성원들은 부모-자식 관계를 가지고 있다
· (신형만, 신봉선, 신용)은 (신형식)이라는 같은 부모를 가지고 있는 형제 관계이다
· (신 홍)의 조상은 선을 타고 위로 올라가면 만나는 (신혁수, 신 용, 신형식)이다
· (신 용)의 자손은 선을 타고 아래로 내려가면 만나는 (신혁수, 신 홍, 신 아)이다
트리의 구조는 위의 가계도와 무척 비슷하다고 볼 수 있습니다
▶노드(node)
☞ 부모노드 (parent) & 자식노드 (child) : 간선으로 연결되어 있음
→ 한 노드의 자손노드 = 그 노드의 서브트리에 있는 노드
☞ 루트노드(root) : 트리의 시작 노드, level=0
☞ 형제노드(sibling) : 같은 부모 노드를 가진 자식 노드들
☞ 조상노드(ancestor) : 간선을 따라 한 노드~루트노드까지에 있는 모든 노드들
☞ 단말노드(terminal) = 리프노드(leaf) : 자식 노드가 없는 노드, 차수=0
☞ 내부노드(internal) : 단말노드 제외한 나머지 노드, 차수=1이상
▶간선(edge)
→ 한 노드의 높이 = 루트~노드까지에 있는 모든 간선의 수
→ 트리의 높이 = 노드의 높이 중 가장 큰 값(최대 레벨)
▶서브트리(subtree) : 자식 노드들이 각각 구성하는 새로운 트리
→ 서브트리의 수 = 자식 노드의 수
▶차수(degree) : 한 노드가 가지는 서브트리의 수(자식노드의 수)
→ 트리의 차수 = 노드의 차수 중 가장 큰 값
▶포리스트(forest) : 여러 개의 트리 집합
다시 이 개념들을 바탕으로 신씨집안 가계부를 트리라고 생각해보면 . .

- 루트 노드 : 신형식
- 단말 노드 : 신짱구, 신짱아, 신봉선, 신 홍, 신 아
- 트리의 전체 높이 : 3 (=신 홍 ~ 신형식 까지 경로에 있는 간선의 수_최대)
- 노드 (신형식)의 차수 : 3 (=자식노드의 수)
- 트리의 차수 : 3 (= 노드의 차수 중 최댓값)
02. 이진트리에 대해
◆ 이진트리(binary tree) : 전체 트리의 차수(노드의 차수 중 최댓값)가 2 이하가 되도록 제한한 트리
※좌우가 구분된다는 특징이 있다!

(b)와 (c)는 모두 자식노드가 하나 밖에 없어 차수가 1로 같지만
둘은 서로 다른 이진트리라는 점!!
☞이진트리는 왼쪽 노드와 오른쪽 노드를 구분한다
이진 트리는 부모-자식 관계의 노드가 하위 레벨에서도 순환적으로 반복되는 계층구조
→ 이진트리의 각 서브 트리 역시 모두 이진트리여야함
<일반 트리를 이진 트리로 변환시키기>
(요건 과제하다가 만든 트리를 좀 변형시킨 일반 트리입니당 쿄쿄..)

① 첫번째 자식 노드 간선 제외한 나머지 간선 제거

② 형제 노드를 간선으로 연결
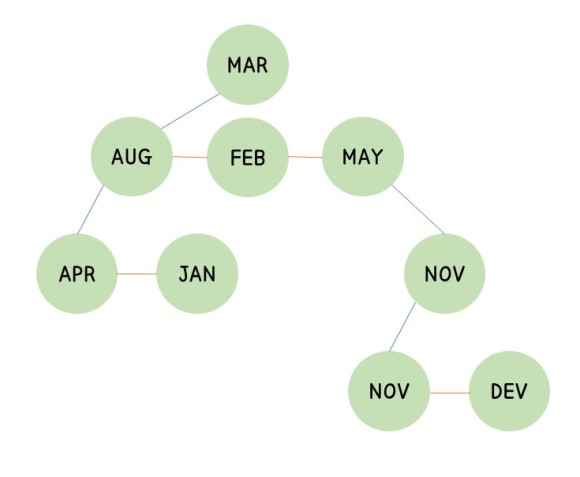
③ 45도(시계) 회전
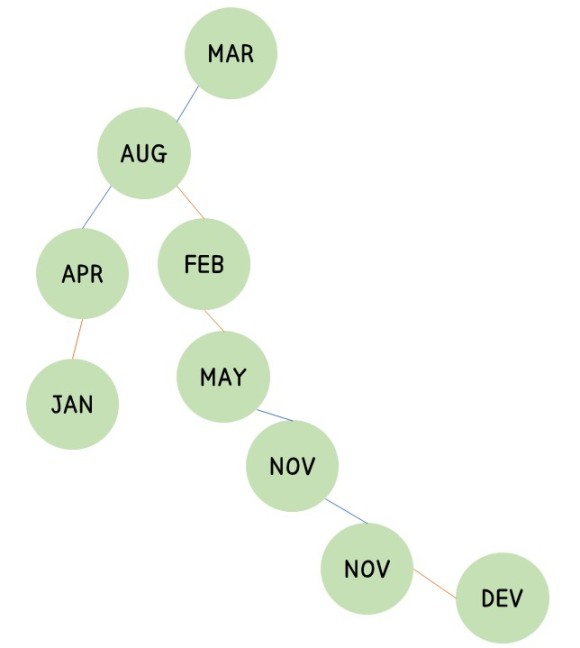
모양새가 좀 빠지긴 하지만 일반트리를 이진트리로 바꾸는 과정입니다!
처음 일반트리였을 때는 트리의 차수가 3이였는데,
마지막에 이진트리로 변환하면서 트리의 차수가 2로 바뀐 걸 확인해 볼 수 있습니다
<이진트리의 특징>
· 노드가 n개인 이진트리 → always 간선은 (n-1)개
- 루트를 뺀 나버지 노드는 부모노드를 하나 가짐
· 높이가 h인 이진트리가 가질 수 있는 노드 개수 : (h+1) ~ (2h+1-1)개
- 한 레벨에 최소 한 개의 노드가 있어야 함 → 최소 h+1
(레벨 0부터 시작, 높이 1부터 시작)
- 한 노드는 자식노드를 최대 2개 가질 수 있음
→ 레벨 i 에서 최대 노드 개수 : 2i
→ 높이 h인 이진트리 전체의 최대 노드 개수
$\sum _{i=0}^h\combi{2}^i=\ \combi{2}^{h+1}-1$h∑i=02i= 2h+1−1
<이진트리 종류>
▶ 포화이진트리(full binarytree)
모든 레벨의 노드가 꽉 찬 포화 상태의 이진트리
→ 높이가 h 일 때, 노드는 (2h+1-1)개 (최대 노드 수)
→ 루트노드를 1번, 하위 레벨로 내려가면서 왼쪽에서부터 차례로 (2h+1-1)번까지 번호를 붙일 수 있다

▶ 완전이진트리(complete binarytree)
높이가 h이고, 노드 수가 n개 일 때 (단, n < 2h+1-1), 노드 위치가 포화이진트리에서의 위치와 완전히 일치하는 이진트리
→ (n+1)번부터 (2h+1-1)까지 모두 공백트리

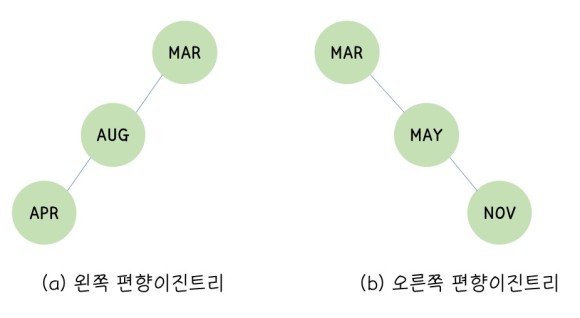
▶ 편향이진트리(skewed binary tree)
최소노드(높이가 h일때, h+1개의 노드)를 가지면서, 모든 노드가 오른쪽 or 왼쪽 방향으로만 서브트리를 가지고 있는 이진트리
'공부 > 자료구조' 카테고리의 다른 글
| 정렬 (1) (0) | 2021.01.22 |
|---|---|
| 그래프 (2) (0) | 2021.01.22 |
| 그래프(1) (0) | 2021.01.22 |
| 트리(3) | 히프 (0) | 2021.01.22 |
| 트리(2) | 이진탐색트리, AVL트리 (0) | 2021.01.22 |




