| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 |
- MongoDB
- 이진탐색트리
- 포렌식워게임
- gitbash
- 뷰
- 자바기초
- 써니나타스
- node
- nodeJS
- 워게임추천
- materialize
- 포렌식
- 웹해킹기초
- 웹해킹
- 자바문제풀이
- Express
- bootstrap
- 이진트리
- GIT
- CTF
- 웹개발
- 그래프
- 웹기초
- node.js
- NavBar
- wargame.kr
- 자바
- mongoose
- 워게임
- 자료구조
- Today
- Total
보안 전공생의 공부
그래프(1) 본문
[출처]
book.naver.com/bookdb/book_detail.nhn?bid=10896666
C로 배우는 쉬운 자료구조
단계별 그림과 삽화로 이론을 다지고 C 언어로 구현해 보는 자료구조 입문서 자료를 구조화하는 다양한 방법을 단계별 그림과 삽화를 곁들여 쉽게 설명하고, 자료구조의 핵심 알고리즘을 C 프로
book.naver.com
목차
01 그래프의 구조 & 용어
02 그래프 순회
03 신장 트리 & 최소 비용 신장 트리
01. 그래프의 구조
◆ 그래프 : 연결되어 있는 원소 사이에 다:다 관계를 표현하는 자료구조
· 정점(Vertex) : 연결할 객체
· 간선(Edge) : 객체를 연결하는 선
그래프 G = ( V, E ) ( V : 정점 집합, E : 간선 집합 )

▶ 무방향 그래프
- 간선 : 방향 無
→ 정점 Vi 와 정점 Vj 을 연결하는 간선 :
( V_ i , V_ j ) = ( V_ j , V_ i )

V(G) = { A, B, C, D }
E(G) = { (A,B), (A,C), (A,D), (B,C), (C,D) }
▶ 방향 그래프
- 간선 : 방향 有
(= 다이그래프)
→ 정점 Vi 와 정점 Vj 을 연결하는 간선 :
V_ i →V_ j : < V_ i , V_ j >
V_ j →V_ i : < V_ j , V_ i >

V(G) = { A, B, C, D }
E(G) = { <A,B>, <A,C>, <B,C>, <C,D>, <D,A> }
▶ 완전 그래프
- 각 정점에서 다른 모든 장점을 연결 → 간선수 최대

· 정점수 n개 일때, 간선수
- 무방향 : n + (n-1) + …+ 2 + 1 = n(n-1)/2
- 방향 : 2 * { n + (n-1) + …+ 2 + 1 } = n(n-1)
▶ 부분 그래프
- 원래 그래프에서 정점, 간선을 일부만 제외해 만듬
→ 그래프 G 와 그래프 G' 의 관계 :
V(G′)⊆V(G)
E(G′)⊆E(G)


▶ 가중 그래프
- 간선에 가중치를 할당함
(= 네트워크)

◆ 그래프 용어

▷ 인접
- 두 정점 Vi , Vj 연결 → 간선 (Vi , Vj) 있을 때
▷ 부속
- 간선 (Vi , Vj) → 두 정점 Vi , Vj 에 부속
예1) 정점 A에 부속된 간선 : (A,B), (A,C), (A,D)
▷ 차수
- 정점에 부속되어 있는 간선의 수
예1) 정점 A에 부속된 간선 수: 3개
- 방향그래프에서는 간선방향에 따라 진입 차수 & 진출 차수 구분함
→ 집입 차수 : 정점을 머리로 하는 간선 수
→ 진출 차수 : 정점을 꼬리로 하는 간선 수
[ 정점의 차수 = 진입 차수 + 진출 차수 ]
예2) 정점 A의 진입차수=1 , 진출차수=2 → 전체차수=3
▷ 경로
- 간선을 따라갈 수 있는 길
- 정점 Vi 에서 Vj까지 연결된 정점을 순서대로 나열한 리스트
- 경로 길이 : 경로 이루는 간선 수
예1) 정점 A → C 경로: A-C , A-B-C , A-D-C 등
경로 A-B-C 의 길이 : 간선 (A,B) , (B,C) → 2
예2) 정점 A → C 경로: A-C
- 단순 경로 : 모두 다른 정점으로 구성된 경로
- 사이클 : 단순 경로 中 시작 정점 = 마지막 정점
예1) 단순경로 A-B-C-D-A
예2) 단순경로 C-D-A-C
- DAG(Directed Acyclic Graph) : 방향그래프 & 사이클 無
▷ 연결
- 정점 Vi 에서 정점 Vj 까지의 경로 有 → Vi , Vj 가 연결되어있음
- 연결 그래프 : 서로 다른 모든 쌍의 정점들 사이에 경로가 있는 그래프
ex ) 트리 = 사이클 無 연결 그래프

연결 그래프
- 단절 그래프 : 연결 X인 정점이 있는 그래프

02. 그래프의 순회
◆ 그래프 순회
- 한 정점에서 시작 → 모든 정점을 한 번씩 방문하는 것
(=그래프 탐색)
① 깊이 우선 탐색 : 시작 정점의 한 방향으로 갈 수 있는 경로가 있는 곳까지 깊이 탐색
더 이상 경로 X → 가장 마지막에 만났던 갈림길 간선이 있는 정점으로 되돌아가 다른 방향의 간선으로 탐색 계속
⇒ 모든 정점 방문
스택(후입선출 구조) 사용
ⅰ) 정점 A부터 탐색 ( 갈림길에서 오름차순 따라 선택)






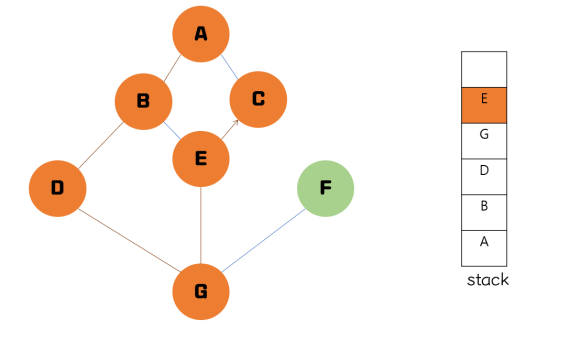
ⅱ) 경로의 끝까지 도달 → 방문하지 않은 인접정점을 가진 정점으로 되돌감


ⅲ) 정점 G에서 방문하지 않은 인접정점 선택해 탐색

ⅳ) 경로의 끝까지 도달 → 방문하지 않은 인접정점을 가진 정점으로 되돌감



ⅴ) 스택 공백 → 탐색 종료

② 너비 우선 선택 : 시작정점에 인접한 정점 모두 차례로 방문
→ 방문했던 정점을 시작으로, 다시 인접한 정점 차례로 방문
⇒ 모든 정점 방문
큐(선입선출 구조) 사용
ⅰ) 정점 A부터 탐색 → 인접 정점 모두 방문
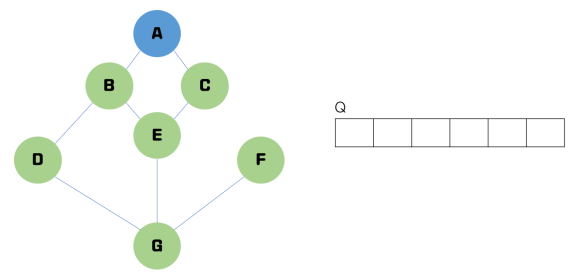

ⅱ) 정점 A의 인접 정점 처리 완료 → 정점 B에 대해 탐색


ⅲ) 정점 B의 인접 정점 처리 완료 → 정점 C에 대해 탐색

ⅳ) 정점 C의 탐색하지 않은 인접 정점 無 → 정점 D에 대해 탐색


ⅴ) 정점 D의 인접 정점 처리 완료 → 정점 E에 대해 탐색

ⅵ) 정점 E의 탐색하지 않은 인접 정점 無 → 정점 G에 대해 탐색

ⅶ) 정점 G에 대해 탐색 → 정점 F에 대해 탐색

큐 공백 → 탐색 종료

'공부 > 자료구조' 카테고리의 다른 글
| 정렬 (1) (0) | 2021.01.22 |
|---|---|
| 그래프 (2) (0) | 2021.01.22 |
| 트리(3) | 히프 (0) | 2021.01.22 |
| 트리(2) | 이진탐색트리, AVL트리 (0) | 2021.01.22 |
| 트리 (1) | 트리, 이진트리 (0) | 2021.01.22 |




